| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Compose
- textfield
- AWS
- Gradle
- Rxjava
- ProGuard
- androidStudio
- 코드포스
- 쿠링
- pandas
- TEST
- Python
- Coroutine
- Kotlin
- android
- boj
- MyVoca
- 프로그래머스
- Codeforces
- architecture
- MiTweet
- 코루틴
- 암호학
- GitHub
- activity
- relay
- 백준
- Coroutines
- Hilt
- livedata
- Today
- Total
이동식 저장소
13주차 1차시 본문
Massey-omura
많이 쓰는 암호는 아니지만, 굉장히 특이한 암호 체계이다. 왜냐고? 아무것도 공유를 안 하거든!
``RSA``에서는 $e$와 $n$을 공유(정확히는 공개)하였다. ``엘가말``에서도 $g^{a}$와 $g^{b}$가 공유된다. 그러나 ``Massey-omura``에서는 송신자와 수신자의 정보가 아무것도 공유되지 않는다.
A가 메시지 송신자, B가 수신자라고 하자. A는 가방에 메시지를 넣고, 가방을 자물쇠로 잠근 후 B에게 가방을 전달한다. 비밀 키 시스템에서는 B가 열쇠를 공유받기 때문에 가방을 열 수 있다. 공개 키 시스템에서는 잠글 수만 있는 키와 열 수만 있는 키가 다르긴 하지만, 어쨌든 B는 자신의 열쇠를 이용하여 가방을 열 수 있다.
그런데 ``Massey-omura``에서는 이런 게 하나도 없다. A는 자신만의 자물쇠와 열쇠를 갖고 있다. B도 자신만의 자물쇠와 열쇠를 갖고 있다.
- A가 가방을 자물쇠로 잠가서 B에게 보낸다.
- B는 그 가방을 자신의 자물쇠로 잠가서 다시 A에게 보낸다.
- A는 자신의 자물쇠와 B의 자물쇠가 모두 잠겨진 걸 확인하고, 자신의 자물쇠를 풀어서 B에게 보낸다.
- 이제 가방에는 B의 자물쇠만 잠겨 있으므로 B는 가방을 열 수 있다.
???
듣고 보면 나름 간단해 보인다. 그러나 ``Massey-omura``는 하나의 메시지를 전송하기 위해 3번의 통신을 해야 하므로 ``RSA``보다는 비효율적이다.
위에서 서술한 과정을 수학적으로 풀어 보자.
- A→B: $m^{e_{a}} \mod p$를 보냄
- B→A: $(m^{e_{a}})^{e_{b}} = m^{e_{a}e_{b}} \mod p$를 보냄
- A→B: $(m^{e_{a}e_{b}})^{d_{a}}=m^{e_{b}} \mod p$를 보냄 $(\because~ e_{a}d_{a}=e_{b}d_{b}=1 \mod p-1)$
- B: $(m^{e_{b}})^{d_{b}}=m \mod p$를 얻음
$p$는 공통의 소수이다. $e$와 $d$는 ``RSA``와 유사한 성질을 갖고 있지만, 서로간에 공유되지 않는다.
여담: 갈루아 체 (Galois Field)
갈루아 필드의 원소는 $x^{2}+x$ 따위의 식이다. 말 그대로 그냥 식이 속한다. 갈루아 필드에 속하는 두 식의 덧셈을 계산할 때, 각 항의 계수는 $\mod n$을 취한다. $n$은 적당한 자연수를 취한다. $n=2$라면 $(x^{2}+1)+(x^{2}+x)=x+1$이다. 곱셈은 두 식을 곱한 결과를 ``적당한 식``으로 나눈 나머지를 취한다. $n$과 ``적당한 식``에 따라 갈루아 체가 Field가 될 수도 있고 안 될 수도 있다. 갈루아 체가 Field라면 갈루아 체는 유한 필드임이 증명되어 있으며 $Z_{n}$보다 훨씬 복잡하지만 계산이 많이 빨라진다.
이 위에서 ``RSA``든 ``엘가말``이든 구현할 수 있다. 이런 걸 ``Eliptic Curve(타원 곡선)``이라고 한다. 타원곡선이 요즘 활발하게 연구된다고 한다. 당장 ``페르마의 마지막 정리``도 타원 곡선을 이용하여 증명되지 않았는가?
Secret Sharing
$n$명이 비밀 값 $x$를 공유하고 있다. 이 시스템의 목적은 $k$명 이상이 협력하면 $x$를 알 수 있지만, $k-1$명 이하가 아무리 협력해도 $x$를 알 수 없도록 하는 것이다.
이 시스템이 성립하려면 ``Trusted Party(신뢰할 수 있는 사람들의 모임)``가 필요하다. 이 조건 때문에 현실에서는 성립하기 힘든 이상적인 시스템이라고 평가받는다.
어쨌든 $k-1$차 다항식 $f(t)=a_{k-1}t^{k-1}+a_{k-2}t^{k-2}+ \cdots + a_{1}t+x \mod m$을 만든다. $n$명의 사람 중 1번 사람에게는 $f(1)$을, 2번 사람에게는 $f(2)$를, ..., $n$번 사람에게는 $f(n)$을 준다. $f(t)$의 미정계수가 $x$까지 포함하여 $k$개이므로, $k-1$개 이하의 값만 가지고는 $f(t)$, 즉 $x$를 온전히 알아낼 수 없다.
그런데 왜 ``Trusted Party``가 필요한가? $x$를 알아내기 위해서는 모든 사람들이 자신이 가진 값을 정확하게 알려줘야 하기 때문이다. 한 명이라도 (의도적이던 아니던) 잘못된 값을 알려주면 $x$를 알아낼 수 없다.
``Secret Sharing``을 이용하여 암호화폐 등을 만들 수 있다. 이론적으로는 가능하다는 말이지, 실제로 사용 가능한 시스템을 만들기는 꽤 어려울 듯.
Zero Knowledge Proof
어떤 사람 $P$가 다른 사람 $V$에게 자신이 $X$에 대한 정보를 알고 있다는 걸 증명하고자 한다. 단, 이 증명 과정에서 $X$에 대한 어떠한 정보도 전달되지 않아야 한다. 즉, $X$를 노출하지는 않으면서 $X$를 알고 있다는 사실을 전달해야 하는 것이다.
네이버에 로그인하는 과정도 위와 같다. 내가 굳이 서버에 비밀번호를 전달할 필요가 없다. 비밀번호를 안다는 사실만 전달하면 되지 않겠는가?
그래프 동형 문제
두 그래프 $G_{1}$과 $G_{2}$가 같은 그래프인가?
그래프의 각 정점에 붙여진 번호가 다르다고 해도 그래프 자체는 같을 수 있다. 즉 $G_{1}$과 $G_{2}$가 동형이라면 $G_{1}$에서 노드의 번호를 적절히 바꾸어 $G_{2}$를 얻을 수 있다.
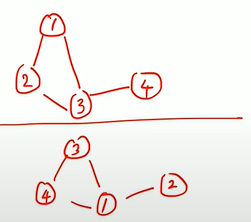
동형 문제는 $NP-Complete$로 알려져 있다. 놀랍게도, 동형 문제가 어렵다는 점을 이용하여 ``Zero Knowledge Proof``를 만들 수 있다.
구체적인 과정
$P$는 동형인 그래프 $G_{1},~G_{2}$를 가지고 있다. 참고로 동형 그래프를 만드는 건 전혀 어렵지 않다. 번호만 바꾸면 되잖아? ㅇㅅㅇ$G_{1}$과 $G_{2}$는 공개해도 상관없다. 그래프 동형 문제가 매우 어렵기 때문에. 대신 $G_{1}$과 $G_{2}$ 사이의 매핑(노드 번호 쌍)은 공개하면 안 된다.
이제 다음의 과정을 반복한다.
- $P$는 $G_{1}$과 동형인 그래프 $G_{temp}$를 만든다.
- $V$는 $G_{1}$과 $G_{temp}$ 또는 $G_{2}$와 $G_{temp}$ 사이의 매핑을 물어본다. 이때 $V$가 둘 다 물어보면 $P$는 대답하지 말아야 한다. $V$가 둘 다 알게 되면 결국 $G_{1}$과 $G_{2}$ 사이의 매핑을 알게 되기 때문.
- $P$는 매핑을 알려준다.
이 과정을 몇 번 반복하면 $V$는 $P$가 매핑을 알고 있다는 사실을 알게 된다. 물론 매핑을 완전히 알 수 있을 만큼 반복하면 안 된다. 따라서 $V$는 매핑을 조금씩 알게 되지만, 매핑을 완전히 알 수는 없다.
정보가 전달되지 않았음을 어떻게 보일 수 있을까? $P$와 $V$가 대화한 흔적을 나중에 $V$가 검토한다고 하자. 사실 $V$는 혼자서 $G_{1}$과 $G_{temp}$를 만들고 위의 과정을 반복할 수 있다. 즉 $P$가 없어도 위의 과정을 똑같이 재연할 수 있다는 뜻이다. 따라서 $P$는 $V$에게 아무런 정보도 넘겨주지 않은 것과 같다. (13강 1주차 37:30~)
사실 이 시스템도 현실적으로 쓰기에는 성능이 별로 좋지 않다. 그래서 현실에서는 적당히 타협하여 사용한다.
수학적인 얘기는 여기까지 하고, 다음 시간부터는 미래의 암호에 대해 이야기하도록 하자.
