| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- pandas
- architecture
- 쿠링
- MyVoca
- Codeforces
- Compose
- TEST
- 코드포스
- 백준
- textfield
- Coroutine
- Gradle
- AWS
- Coroutines
- 코루틴
- Hilt
- GitHub
- 암호학
- activity
- Rxjava
- 프로그래머스
- Kotlin
- Python
- MiTweet
- android
- boj
- ProGuard
- livedata
- androidStudio
- relay
- Today
- Total
이동식 저장소
1022. 소용돌이 예쁘게 출력하기 본문
오랜만에 문제를 하나 풀어보자.
1022번: 소용돌이 예쁘게 출력하기
첫째 줄에 네 정수 r1, c1, r2, c2가 주어진다.
www.acmicpc.net
주어진 규칙으로 채워지는 격자의 일부분을 출력하는 문제이다.
격자의 크기가 $10,000 \times 10,000$이므로 격자를 미리 채우는 방법은 시간도 오래 걸리고, 문제의 의도에도 맞지 않다. 이 문제의 의도는 격자에 쓰인 수를 좌표만 가지고 구하는 것이다.
격자를 관찰해 보면, 중심이 같은 정사각형으로 이루어져 있다는 사실을 알 수 있다.
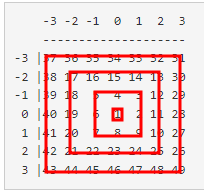
임의의 점 $(r,~c)$과 $(0,~0)$ 사이의 유클리드 거리는 $\max(|r|,~|c|)$이다. 이 값을 $d$라고 하고, $(r,~c)$가 속한 정사각형의 지름이라고 부르자. 수학적으로는 존재하지 않는 말이지만, 이 문제를 풀 때만 사용하겠다.
지름이 $d$인 정사각형에는 다음 범위의 수가 적혀 있다.
- $d=0:~[1,~1]$
- $d=1:~[2,~9]$
- $d=2:~[10,~25]$
- $d=3:~[26,~49]$
- $ \vdots $
- $d=d_{0}:~[(2 d_{0}-1)^{2} + 1,~(2 d_{0}+1)^{2}]$
따라서 $d$를 알면 해당 좌표에 적힌 수의 범위를 알 수 있다. 이제 수를 정확히 계산하는 방법을 생각해 보자.
각 정사각형에서 제일 작은 수가 적혀 있는 좌표를 ``정사각형의 시작점``이라고 하자. $d>0$일 때 정사각형의 시작점은 다음과 같다.

순서대로 나열하면 $(0,~1),~(1,~2),~(2,~3),~\cdots$이다. 즉 $d=d_{0}$인 정사각형의 시작점은 $(d_{0}-1,~d_{0})$이고, 여기에는 $(2n-1)^{2}+1 = 4n^{2}-4n+2$가 쓰여 있다. 이제 정사각형을 다음과 같이 네 부분으로 나눌 수 있다.
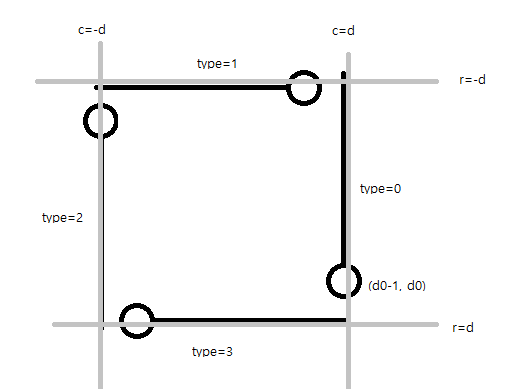
점 $(r,~c)$가 각 타입에 속하는 조건은 다음과 같다.
$$\begin{cases}r=d_{0},~c>-d_{0} & (type = 3)\\c=-d_{0},~r>-d_{0} & (type=2) & \\r=-d_{0},~c<d_{0} & (type=1) \\ c=d_{0},~r<d_{0} & (type=0)\end{cases}$$
$type$별 시작점(위 그림에서 동그라미로 표시한 좌표)에 쓰인 수 $b$는 다음과 같다.
$$b=\begin{cases}4n^{2}+2n+2 & (type = 3)\\4n^{2}+2 & (type=2) & \\4n^{2}-2n+2 & (type=1) \\ 4n^{2}-4n+2 & (type=0)\end{cases}=4n^{2}-4n+2+(2n \times type)$$
$type$별 시작점과 $(r,~c)$ 사이의 거리 $res$는 다음과 같다.
$$res=\begin{cases}c+(d_{0}-1) & (type = 3)\\r+(d_{0}-1) & (type=2) & \\-c+(d_{0}-1) & (type=1) \\ -r+(d_{0}-1) & (type=0)\end{cases}$$
따라서 $(r,~c)$에 적혀있는 수 $N=b+res$이다. 이제 각 점에 대해 $N$을 구하면 된다. 단, $(r,~c)=(0,~0)$일 때 $N=1$이다.
한 가지 주의할 점은, 출력 형식에서 수의 자릿수를 맞추고 있다는 것이다. 자릿수가 작은 수는 앞에 공백을 추가로 출력해야 한다. 언어별로 적절히 처리하면 되겠다.

'Problem Solving > BOJ' 카테고리의 다른 글
| 17619. 개구리 점프 (0) | 2024.03.22 |
|---|---|
| 12920. 평범한 배낭 2 (1) | 2023.07.30 |
| 26607. 시로코와 은행털기 (0) | 2023.07.29 |
| 2094. 강수량 (0) | 2023.06.14 |
| 14922. 부분평균 (0) | 2023.05.02 |




