| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Kotlin
- androidStudio
- textfield
- TEST
- 코루틴
- Hilt
- relay
- livedata
- android
- 백준
- MiTweet
- activity
- Python
- MyVoca
- GitHub
- ProGuard
- 쿠링
- architecture
- Codeforces
- Compose
- AWS
- Rxjava
- 암호학
- boj
- Gradle
- 프로그래머스
- pandas
- Coroutine
- 코드포스
- Coroutines
- Today
- Total
이동식 저장소
1184. 귀농 본문
주말 특집 플래티넘 풀이 시간!
1184번: 귀농
상근이와 선영이는 도심 속의 삶에 싫증을 느꼈고, 친구 현수가 있는 시골로 농사를 지으려 내려왔다. 현수의 땅은 크기가 N×N 인 정사각형이고, 땅은 단위 정사각형 1×1로 나누어져 있다. 각 단
www.acmicpc.net
합이 같고 한 점에서만 만나는 두 직사각형 구역의 쌍이 몇 개 있는지 구하는 문제이다.
두 직사각형이 한 점에서 만나는 경우는 빨간 기준점을 기준으로 좌상-우하 방향에서 만나는 경우와 좌하-우상 방향에서 만나는 경우 두 가지이다.
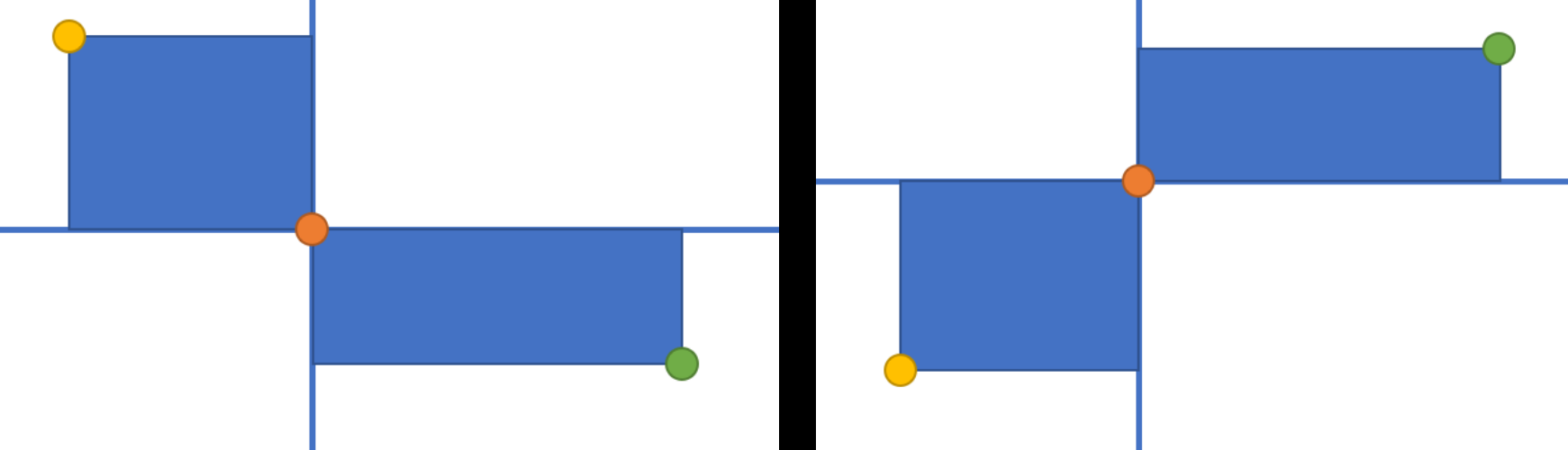
따라서 기준점을 먼저 잡은 후, 좌상-우하 두 방향에서 만들 수 있는 모든 직사각형의 쌍을 비교하고, 좌하-우상 방향으로도 동일하게 비교하면 된다. 참 쉽죠?
쉽지 않다
위의 풀이를 어떻게 구현할 것인가? 직사각형을 결정하려면 대각선을 이루는 두 점을 결정해야 한다. 따라서 일반적으로 직사각형 두 개를 결정하려면 점을 4개 결정해야 하지만, 이 문제에서는 두 직사각형이 하나의 점을 공유하므로 점을 3개만 결정해도 된다. 그런데 점을 결정하려면 좌표 2개를 결정해야 하므로, 결국 좌표 6개를 결정하는 문제가 된 것이다.
점 6개를 결정하는 가장 쉬운 구현은 6중 반복문이다. 그런데 이렇게 구현하면 시간복잡도가 $N^{6}$에 비례하므로 당연히 시간 초과이다. $N=50$으로 계산해 보면 $N^{4}$까지는 통과할 수 있을 듯.
점 3개를 $N^{4}$ 시간에 결정할 수 있는가? 아니, 결정할 수 없다. 그렇다면..
결정하지 않으면 된다
점 하나당 시간이 $N^{2}$라고 하면, $N^{4}$ 시간엔 점을 2개 결정할 수 있다.
놀랍게도 모든 점을 동시에 결정할 필요는 없다. 왜냐하면 지금 구하고 싶은 건 직사각형 그 자체가 아니기 때문이다. 직사각형의 합만 잘 계산하고, 왼쪽과 오른쪽에서 합이 몇 개나 겹치는지 구하기만 하면 된다.
따라서 점 3개를 동시에 결정하는 대신 점 2개를 2번 결정하면 된다. 빨간 점과 노란 점을 결정하여($N^{4}$) 왼쪽 방향에서의 모든 합을 계산하고, 이어서 빨간 점과 초록 점을 결정하여 오른쪽 방향에서의 합을 계산하자. 이제 오른쪽 합과 왼쪽 합이 몇 개나 같은지 세면 된다.
반복문 배분만 잘 하면 되는 문제. 구현량이 많긴 하지만 솔직히 플5는 아닌듯.

'Problem Solving > BOJ' 카테고리의 다른 글
| 17616. 등수 찾기 (0) | 2022.08.15 |
|---|---|
| 3830. 교수님은 기다리지 않는다 (0) | 2022.08.14 |
| 14711. 타일 뒤집기 (Easy) (0) | 2022.07.25 |
| 1014. 컨닝 (0) | 2022.07.19 |
| 22343. 괄호의 값 비교 (0) | 2022.07.04 |




