| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Codeforces
- Compose
- textfield
- Gradle
- ProGuard
- Kotlin
- 코드포스
- relay
- 암호학
- Coroutines
- 프로그래머스
- MyVoca
- boj
- livedata
- architecture
- Rxjava
- Python
- MiTweet
- pandas
- androidStudio
- GitHub
- 코루틴
- activity
- TEST
- AWS
- android
- 백준
- Coroutine
- 쿠링
- Hilt
- Today
- Total
이동식 저장소
3830. 교수님은 기다리지 않는다 본문
왜냐고? 그것이 교수님이니까..
3830번: 교수님은 기다리지 않는다
교수님의 질문 (? a b)이 입력으로 들어올 때 마다, 지금까지 측정한 결과를 바탕으로 a와 b의 무게 차이를 계산할 수 있다면, b가 a보다 얼마나 무거운지를 출력한다. 무게의 차이의 절댓값이 1,000,
www.acmicpc.net
2년 전에 못 푼 문제라 다시 도전해 봤는데, 그때의 내가 못 푼 이유가 있구나... 도저히 풀지 못할 것 같아 답을 봤다. 이 글은 타인의 풀이를 공부하여 정리한 것이다.
몇몇 물체간의 무게 관계가 주어졌을 때, 현재 가지고 있는 정보만으로 두 물체의 무게 차이를 구할 수 있는지, 구할 수 있다면 그 값은 몇인지 구하는 문제이다. 골드와 플레 실력을 나누는 쿼리 문제.
흠... 언뜻 보면 LCA라고 생각할 수도 있지만, LCA는 트리에서만 적용할 수 있다. 이 문제에서는 트리가 아닌 그래프가 주어질 수 있으므로 LCA를 사용할 수 없다.
관계의 집합이라면 역시 union find겠군. 근데 너무 어려워 보이는데....
첫 번째 시도
당연히 안 될 것 같지만, 쿼리가 주어질 때마다 위상 정렬을 수행해 보자. ``a b w``가 주어질 때 ``b``에서 ``a``로 가는 길이 ``w``인 간선을 연결하고, 쿼리가 주어지면 위상 정렬을 통해 ``dw[i]``를 계산하자.
``dw[i]``: ``i``번 물체는 루트보다 얼마나 더 무거운가?
쿼리가 몇 개나 주어질 지 모르겠지만, 시간복잡도가 $O(NM)$이라 당연히 시간 초과일 것 같다.

두 번째 시도
흠.... 역시 union find가 맞군. 쿼리를 수행할 수 있는 union find를 짜야 한다.
위에서처럼 ``dw[i]``에 ``i``번 물체가 루트보다 얼마나 무거운지를 저장하자. 이렇게 하면 루트가 가장 가볍고, 아래에 위치하는 물체는 상대적으로 더 무겁다고 생각할 수 있다.
어려운 문제를 풀 땐 그림을 그려 보자.
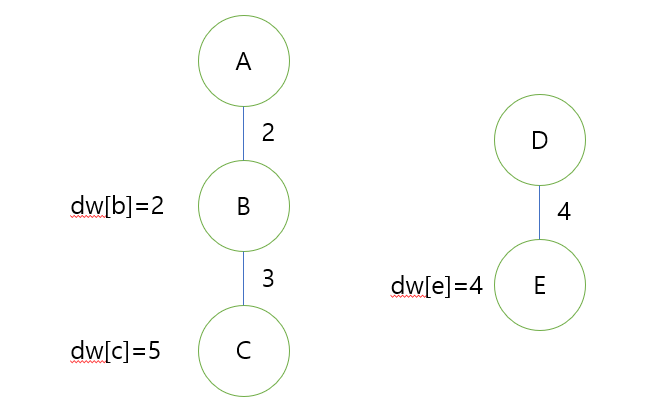
그림처럼 두 개의 disjoint set이 존재한다. 왼쪽 set의 루트는 A이고, A보다 무거운 물체 B, C가 집합에 속해 있다. 마찬가지로 오른쪽 set에도 D를 루트로 하여 D보다 4만큼 더 무거운 물체 E가 존재한다.
``! c e w`` 쿼리가 주어졌을 때 어떤 일이 일어나는지 생각해 보자.
``c e w``는 ``e``가 ``c``보다 w만큼 더 무겁다는 뜻이다. 집합에서 무거운 물체가 밑으로 가야 하므로 병합 후의 집합은 대충 이렇게 생겼을 것이다.
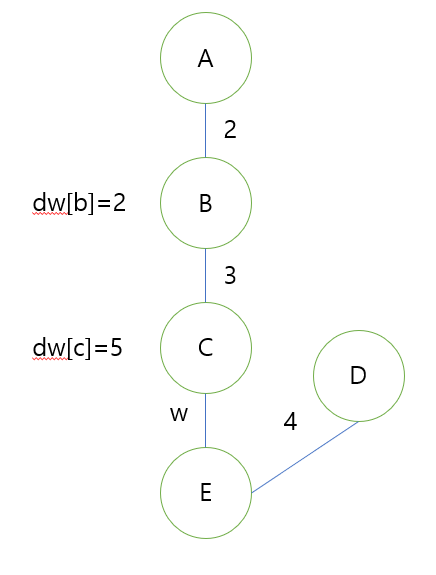
D는 E보다 4만큼 가볍다. 물체 E는 C보다 w만큼 가벼우므로 $dw[d] = dw[c] + w - 4 = dw[c] + w - dw[e]$이고, $dw[e] = dw[c] + w$이다. $dw[d]$를 먼저 갱신해야 함에 유의하자.
D를 $root[e]$로 추상화할 수 있으므로, ``! c e w``를 업데이트하는 최종 식은 $dw[root[e]] = dw[c] + w - dw[e]$이다.
find는?
merge는 위에서 말한 대로 구현하면 된다. 그럼 find는?
Union find에서 find 함수는 부모를 재귀적으로 갱신한다. 위의 그림을 다시 보자.

초기 상태에서 ``! a b 2``와 ``! b c 3`` 쿼리가 주어졌다면, 쿼리 2개가 주어진 직후 $root[b] = a$, $root[c] = b$이다. find 함수는 $root[b]$와 $root[c]$를 모두 $a$로 업데이트한다.
int find(int n)
{
if (root[n] == n)
return n;
return root[n] = find(root[n]);
}나의 루트는 (나의 루트)의 루트라는 코드이다.
잘 생각해 보면 같은 방식으로 $dw[n]$을 업데이트할 수 있다. 업데이트 전 $dw[n]$은 나와 인접 부모간의 거리이다. 정확히는 무게의 차이이지만 설명을 위해 거리라고 말하겠다.
나와 인접 부모간의 거리를 나타내던 $dw[n]$은 나와 진짜 부모 사이의 거리로 업데이트돼야 한다. 위의 그림으로 설명하자면 처음에 $dw[c]$는 $c$와 $b$(인접 부모) 사이의 거리였지만, 업데이트가 완료된 후에는 $c$와 $a$(진짜 부모) 사이의 거리를 나타내야 한다.
재귀적으로 $c$와 $a$ 사이의 거리는 $c$와 $b$ 사이의 거리(나와 인접 부모 사이의 거리)와 $b$와 $a$ 사이의 거리(인접 부모와 진짜 부모의 거리)의 합으로 생각할 수 있다. 식으로 나타내면 $dw[n]$은 나와 인접 부모 사이의 거리 $dw[n]$ + 인접 부모와 진짜 부모 사이의 거리 $dw[root[n]]$으로 나타낼 수 있다. 그런데 $dw[root[n]]$은 ``find(root[n])``을 실행하면 재귀적으로 계산된다. 따라서
- ``find(root[n])``을 실행하여 결과를 ``parent``에 저장한다. ``parent``는 위에서 말한 진짜 부모이다.
- $dw[n] += dw[root[n]]$을 실행한다. 인접 부모와 진짜 부모 사이의 거리를 더해준 것이다.
- ``root[n]``에 ``parent``를 대입한다.
이렇게 하면 부모와 거리 모두 재귀적으로 업데이트할 수 있다.
int find(int n)
{
if (root[n] == n)
return n;
auto parent = find(root[n]);
dw[n] += dw[root[n]];
return root[n] = parent;
}
void merge(int a, int b, int w)
{
int root1 = find(a), root2 = find(b);
if (root1 == root2)
return;
// merge weight
dw[root2] = dw[a] + w - dw[b];
root[root2] = root1;
}merge는 뭐 그대로 구현하면 되고..
정리
요약하면 다음과 같다.
- Union find는 항상 재귀적으로 생각해야 한다. (중요)
- Union find에서 나의 값을 계산하려면 1) 나와 인접 부모 사이의 값과 2) 인접 부모와 진짜 부모 사이의 값을 고려해야 한다.
- ``b``를 ``a``에 병합하려면, ``b``를 ``a``에 연결한 후 원래 ``b``와 연결되어 있던 부분을 병합하자. ``find``로 이은 후 ``merge``로 완성한다고 생각하면 된다.

친구한테 물어봤더니 조금만 응용하면 된다고 하는데.. 그 조금이 실력이거늘..
'Problem Solving > BOJ' 카테고리의 다른 글
| 9938. 방 청소 (1) | 2022.08.16 |
|---|---|
| 17616. 등수 찾기 (0) | 2022.08.15 |
| 1184. 귀농 (0) | 2022.07.31 |
| 14711. 타일 뒤집기 (Easy) (0) | 2022.07.25 |
| 1014. 컨닝 (0) | 2022.07.19 |




